Newton was wrong about Light ! But so was everyone else
Chronicles of Wave-Particle Duality and the quest for finding the true nature of light
Descartes changed the landscape of optics. Completely.
Until Kepler, understanding vision guided the study of the nature of light.
René Descartes (1590–1650) was the first person to explore intrinsic nature of light and the laws of optics for themselves.
His work laid the foundation for Newton and his sucessors.
But for that, we first need to know about Fermat.
Fermat
Fermat’s fame had little to do with his work on optics.
Yet the leading mathematician of 17th century made a major contribution to optics as well by his derivation of Snell’s law using the principle of least time.
This is how Feynmann put the principle of least time :
‘His idea is this: that out of all possible paths that it might take to get from one point to another, light takes the path which requires the shortest time.’
1400 years ago, Hero of Alexandria had derived the law of reflection, on a similar basis of the principle of least distance.
The fact that it yields the correct Snell’s law hints us at the inherent relation of this principle with the nature of light.
Newton
Particle Nature of Light
Who doesn’t know Newton ?
From his laws of motion to that of Gravitation, Newton revolutionised physics in numerous and equally important ways.
Interestingly however, all of his remarkable experimental contributions to physics are in the field of optics.
- Newton’s Theory of Colour
Like with many other things, Newton was also the first to show that the colour is the property of light and not of the medium.
He was able to show experimentally, with the help of a glass prism, that the light generated by Sun consisted of all the colours. Each of these colours bends by a slightly different amount on passing through the prism - red bends the least and violet the most.
But, it is not this splitting of light that made Newton the legend he was.
For the ability of glass prisms to generate multiple colours was known since antiquity. It is just that this phenomenon was not attributed to light. Instead, colour was considered as a characteristic of the material.

Dispersion of white light into colours by a glass prism
(Source : http://labman.phys.utk.edu/phys222core/modules/m7/dispersion.html)
Newton showed that when a particular colour was passed through the prism, no such dispersion took place. Moreover, when these colours were combined together white light was obtained.
This proved that white light consisted of all the colours.
- Designing the first Reflecting Telescope
In Newton’s time, the telescopes were made using lenses.
Such ‘refracting telescopes’ suffered from a major problem - chromatic aberration.
Chromatic aberration is a phenomenon in which light rays passing through a lens focus at different points, depending on their wavelength. For a telescope to make bright images of distant objects, it needs lenses of increasingly large apertures to gather enough light.
But any lens of sufficiently large aperture is bound to face aberrations.
That is where Newton comes in.
Newton designed a reflecting telescope where incoming light is reflected by a concave mirror onto a plane mirror that reflected the light to the observer. This design works like a charm and decreases susceptibility to chromatic aberrations.
So much so, that every major telescope today is a modified version of Newton’s reflecting telescope.
- Particle Nature of Light
Despite these successes, Newton was yet to answer the biggest question of them all.
What IS Light ? What is it made of ?
Newton developed and advocated a corpuscular theory of light. According to him, light is made up of tiny particles called corpuscles. Every source of light emits a massive number of these ‘corpuscles’ in a medium surrounding the source.
Moreover, these corpuscles had to be perfectly elastic, rigid, and weightless.
Interestingly, when Newton was advocating for a corpuscular theory of light, researchers had been gathering more and more evidence that supported its wave nature. For instance, Francesco Grimaldi made the first observation of diffraction of light.
Light source emitting corpuscles
(Source : https://scienceready.com.au/pages/particle-and-wave-model-of-light)
Diffraction here, refers to the slight bending of light as it passes around the edge of an object.
As per Grimaldi, when light passed through a hole, it did not follow a rectilinear path as would be expected if it consisted of particles. Instead it took on the shape of a cone. Newton explained this observation by stating that diffraction was only a special case of refraction that was caused by the ethereal atmosphere near the surface of the bodies.
Moreover, Newton’s theory could also explain reflection.
However he could only explain refraction by assuming (that too incorrectly) that light accelerated upon entering a denser medium because somehow the gravitational pull on it was stronger.
Future works, however, contradicted his findings.
Huygens (1629–1695)
Wave Nature of Light
In 1679, Olaus Romer determined that the speed of light is finite.
Christian Huygens was a contemporary of Newton who suggested a wave theory of light. Romer’s result was a crucial ingredient to his theory, which Huygens published in his Traite de la Lumiere (Treatise on Light) in 1690.
For him light waves were just like sound waves.
The latter travelling through air while the former travelled through ether. Huygens explained the finite speed of light by the elastic collisions of a succession of spheres that he believed made this ether.
Thus, according to Huygens, light was a longitudinal wave.
Later studies by Fresnel and Maxwell, however, dismissed this claim and showed that light waves are actually transverse waves.
Huygens proposed that every point reached by a luminous disturbance becomes a source of a spherical wave. The sum of these ‘secondary wavelets’ determines the form of the wave at any subsequent time. This is called the Huygens-Fresnel principle.
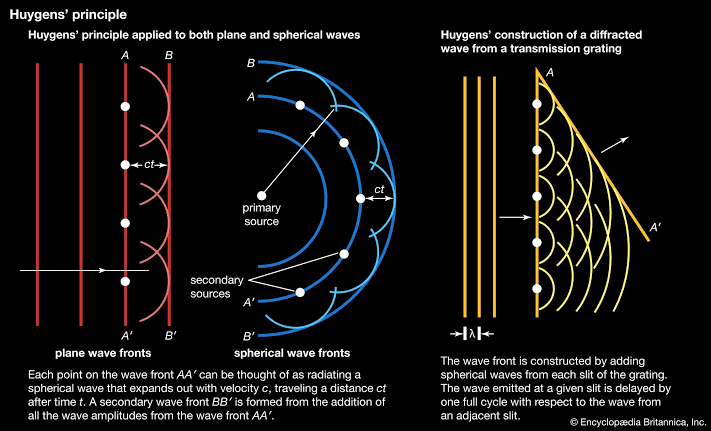
Wavefront determined by the sum of secondary wavelets
(Source : https://www.britannica.com/science/Huygens-principle)
However, the assumption that the secondary waves travelled only in the ‘forward’ direction is not explained in his theory.
Young (1773–1829)
Double Slit Experiment
Till now Newton’s corpuscular theory had only been challenged on the theoretical front.
But in 1802, Thomas Young pushed it back even further with his conclusive demonstration of the wave nature of light.
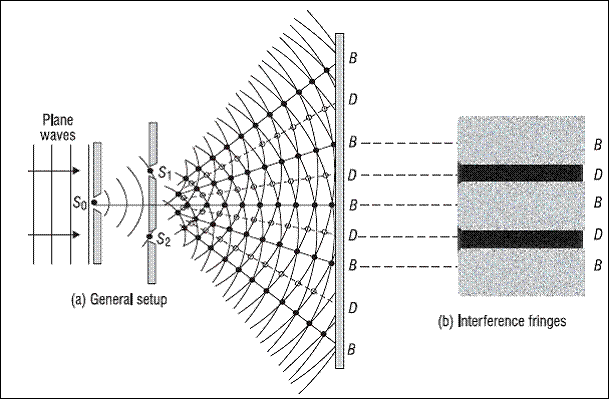
And he did so with his landmark double-slit experiment. Using a mirror, Young directed a beam of light from a narrow slit in a window pane of his lab onto a simple apparatus.
This results in an interference pattern that only waves can produce.
By repeating his experiment, Young could relate colour and wavelength, and was thus able to calculate approximately the wavelengths of the seven colors recognized by Newton that composed white light.
For recreating the double-slit experiment, we use two slits that are illuminated by the quasi-monochromatic light of a single laser.
If the width of the slits is much less than the wavelength of the laser light, the slits diffract the light into cylindrical waves. The superposition of these two cylindrical wavefronts determine the amplitude and consequently the intensity of light at every point on the screen. The difference in phase (phase difference) between the two waves is determined by the difference in the distance travelled (path difference) by the two waves.
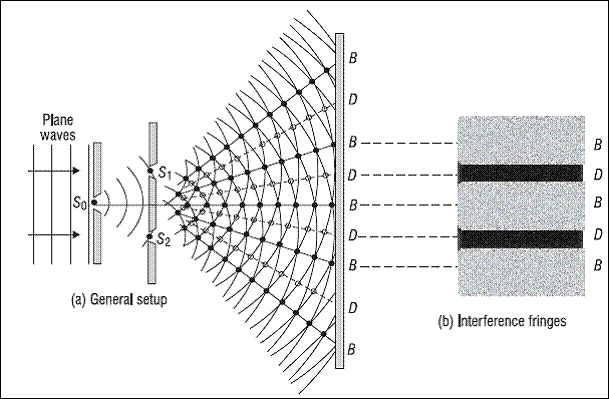
Interference pattern forrmed in Young’s Double Slit Experiment
Thomas Young dared to debunk the corpuscular theory of light. A challenge indeed, given the formidable dominance of Newton’s ideas at the time.
Nevertheless, wave theory eventually found broad acceptance, particularly through the works of Fresnel in France.
Fresnel (1788–1827)
Theory of Diffraction and Polarisation of Light
Augustin Jean Fresnel was Young’s ‘partner in crime’.
His work on diffraction of light championed the wave nature of light. Fresnel began by undertaking experiments with diffraction.
He noted that when light passed through a diffractor, one could see a series of dark and bright bands behind the diffractor. However when one edge of the diffractor was blocked, the bright bands within the shadow vanished and the bright bands remained only on the unblocked side of the diffractor.
From this, Fresnel concluded that the bright bands in the shadow were produced by light coming from both edges. When one edge was blocked, the bright bands resulted from the reflection of light from the other edge of the diffractor.
Fresnel was able to develop a mathematical theory for these observations.
The theory based on the wave nature of light and could predict the position of bright and dark lines based on whether the vibrations were in phase or out of phase.
He published his first paper on wave theory of diffraction in 1815.
In 1819, Fresnel presented his work on wave theory of diffraction in a competition by the French Academy of Sciences. The committee of judges, headed by Francois Arago, included Jean-Baptiste Biot, Pierre-Simon Laplace, and Simeon-Denis Poisson.
They were all prominent advocates of Newton’s corpuscular theory. Yet, Poisson was impressed by Fresnel’s submission and extended his calculations to come up with an interesting consequence :
“Let parallel light impinge on an opaque disk, the surrounding being perfectly transparent. The disk casts a shadow - of course - but the very center of the shadow will be bright. Succinctly, there is no darkness anywhere along the central perpendicular behind an opaque disk (except immediately behind the disk)”.
According to the corpuscular theory, however, there could not be such a bright spot behind the disk.
As Chair of the Committee, Arago asked Fresnel to verify Poisson’s prediction and you know what; Fresnel found the bright spot right where it was predicted.

Poisson spot in the shadow of a ball bearing formed by a laser
(Source : https://web.physics.ucsb.edu/~lecturedemonstrations/Composer/Pages/84.12.html)
This ‘Poisson spot’ won Fresnel the competition. But more importantly, discovery put the wave theory of light on an even more serious footing.
Even still, some researchers were skeptical.
Polarized light is a kind of light is made up of waves that vibrate in only in a single plane.
Despite the triumph of the wave theory of light in explaining interference and diffraction, the properties of the polarized light still provided a strong argument in favor of the corpuscular theory. Moreover, wave theory was yet to explain any of these properties.
Thus, Fresnel and Arago sought to do the same using Fresnel’s theory. In 1817, Fresnel became the first person to obtain circularly polarized light.

Circularly Polarised Light
(Source : https://en.m.wikipedia.org/wiki/Circular_polarization)
The only hypothesis that could explain the experimental results found by the duo was that light is a transverse wave.
So, in 1821, Fresnel published a paper in which he claimed that light is a transverse wave. Young had independently reached the same conclusion. Fresnel could explain the double refraction from his transverse wave hypothesis.
Double refraction refers to the splitting of a single ray of unpolarized light entering an anisotropic medium into two rays, each traveling in a different direction.
Thus the status of light as a transverse wave was sealed.
Maxwell
Electromagnetic Waves
Maxwell’s wasn’t even an optical physicist.
He was simply trying to make sense of the mess electricity and magnetism were at the time. Michael Faraday had told us that magnetic field changing over time yielded some electric force. The asymmetry of this relation, however, bothered Maxwell to the extent that he felt that change of electric field should similarly result in a magnetic field.
One thing led to another and he eventually added a term in the Ampere’s Circuital Law.
It is this term that corresponds to a time rate of change of the electric field. This addition immediately yielded a wave equation for an electromagnetic wave.
Surprisingly, these waves seemed to propogate at 3×10^8 m/s.
The speed of light.
And just like that, we were enlightened about the undulations of mutually perpendicular electric and magnetic fields propagating in space that produced (or rather were themseleves) the most ubiquitous source of energy in the universe. The direction of propagation was perpendicular to both the electric and magnetic fields.
Maxwell’s results were published in 1865.
Thus, the light waves were shown to be transverse waves, just as Young and Fresnel had claimed; as opposed to the longitudinal wave propagating through ether medium, a picture adopted by Huygens.
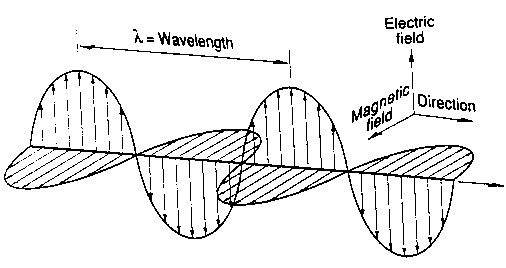
Undulations of mutually perpendicular Electric and Magnetic fields produces electromagnetic waves
(Source : https://www.geo.mtu.edu/rs/back/spectrum/)
In 1888, Heinrich Hertz experimentally demonstrated that light was truly an electromagnetic wave.
Planck (1858–1947)
Blackbody Radiation
In 1893, Wien applied the laws of thermodynamics and electromagnetism to the problem of blackbody radiation.
His law, Wein’s distribution law (now just an approximation) accurately described the short-wavelength (high-frequency) spectrum of thermal emission from objects. But it failed to accurately fit the experimental data for long-wavelength (low-frequency) emission.
An alternative proposed was the Rayleigh–Jeans formula.
It gave results in agreement with the experimental observations at low frequencies. However, it failed miserably at high frequencies. The radiancy, according to Rayleigh and Jeans, is inversely proportional to the fourth power of the frequency, which indicates that at high frequencies the radiancy will approach infinity. Thus, leading to unphysical results in the ultraviolet region of the spectrum.
This failure is known as the Rayleigh–Jeans ultraviolet catastrophe.
The conclusion of such unphysical predictions by arguments based on classical physics and thermodynamics made researchers question the same.
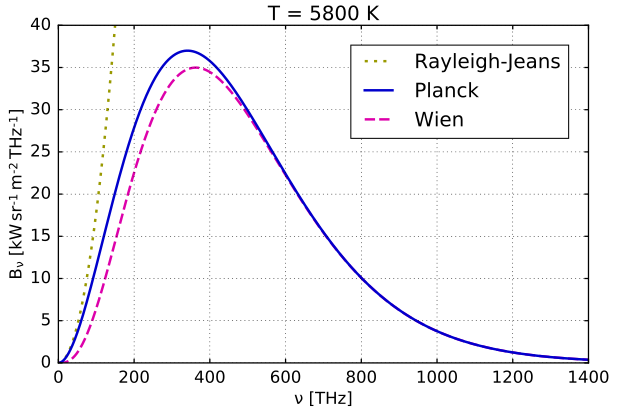
Comparison of Planck’s law with Wien approximation and Rayleigh-Jeans law
(Source : https://en.m.wikipedia.org/wiki/Rayleigh%E2%80%93Jeans_law)
However, at this point Max Planck stepped in.
He calculated the entropy of the linear oscillators and showed that the expression for entropy in the thermodynamic step could only be recovered if he assumed the total energy of the oscillators was made up of finite energy elements. Each of these elements must have an energy ε that is equal to nℏυ.
(Here n is an integer and ℏ is the Planck’s constant.)
This last step was a departure from classical physics in two ways :
- It postulates that energy is proportional to frequency, not amplitude, as would be expected for a classical oscillator.
- For a given frequency υ, the energy is quantized, i.e., it comes in units of ℏυ.
Planck’s derivation for the black-body spectrum was based on the quantization of the material of the cavity and NOT the radiation itself. Moreover, Planck later described it as “an act of desperation” to get the correct expression that agreed with experiments.
However, the idea still had far reaching consequences for the ultimate description of the nature of light.
Einstein
Photon
Einstein re-introduced the particle nature of light.
And he did so, while giving Planck’s hypothesis a new and bold meaning.
Photoelectric effect is the emission of electrons from a metallic surface irradiated by light. In his 1905 paper on the same, Einstein postulated that light comes in discrete bundles, or quanta of energy, borrowing Planck’s hypothesis.
Let’s see what just happened.
On the one hand, interference and diffraction experiments required a wave nature of light for their explanation. While the photoelectric effect could only be understood by invoking a particle type picture.
It was only after almost a quarter century that a complete resolution and the formal theory to rigorously explain all these phenomena would be found.
A theory involving the infamous quantum mechanics.
Dirac (1902–1982)
Quantum Theory of Light
The birth of quantum mechanics took place in 1925.
Through the works of Werner Heisenberg, Max Born, Pascual Jordan, and Paul Dirac, on one hand, and Erwin Schrodinger, on the other; this new theory replaced both Newton’s and Maxwell’s ideas.
An important underlying feature of the new theory was the notion of complementarity.
Namely two observables are complementary if precise knowledge of one of them implies that all possible outcomes of measuring the other one are equally probable. This injected the notion of wave-particle duality in the discourse on the nature of both light and matter.
Since Einstein’s insight in 1905, another phenomena requiring particle nature of light had emerged. This was, the excitation of an atom by absorbing a photon.
In 1927, Paul Dirac settled the debate by synthesizing the wave and particle natures of light in a single theory.
According to Maxwell’s theory, the light consisted of electromagnetic waves of different frequencies. The oscillating waves could be interpreted as simple harmonic oscillators.
But not the classical ones.
Each mode of the electromagnetic field had to be a quantized simple harmonic oscillator.
Yet, quantum electrodynamics also permits a particle perspective on light. It follows from the annihilation and creation operators which are subject to the appropriate commutation relation.
(These are mathematical operators which come up in the study of quantum harmonic oscillators and many-particle systems)
This means that, according to Dirac, particle and wave pictures are not competing models for the nature of light.
Rather, they are complementary.
Thus, light embeds in itself, a wave-particle nature.
References
- Optics in Our Time by Mohammad D. Al-Amri, Mohamed M. El-Gomati, M. Suhail Zubairy
- https://en.m.wikipedia.org/wiki/Isaac_Newton
- https://en.m.wikipedia.org/wiki/Huygens%E2%80%93Fresnel_principle
- https://en.m.wikipedia.org/wiki/Double-slit_experiment
- https://en.m.wikipedia.org/wiki/Creation_and_annihilation_operators
