When 3’s Really a Crowd
The 3 Body Problem Revisited
Newton rarely left anything unsolved.
He himself posed the two-body problem and solved it in his Principia published in 1687. The problem was concerned with the motion of 2 bodies under the force of their mutual gravitational attraction.
This question involves solving a system of second-order differential equations.
It is these differential equations which determine an object’s future motion from its current position and velocity. When we say Newton solved the 2 body problem, we mean that he found the solution to these differential equations.
A natural extension, one might consider, would be a system of 3 bodies moving under the influence of their mutual gravitational attraction.
This is our 3 body problem.
And similar to its precursor, its solution involves solving for another system of differential equations. But, contrary to our intuition, the methods Newton employed to solve his two object system do not lead us much further in this pursuit.
So, we first try to tackle simpler cases.
Reduced 3 Body Problem
Notice that the mass ratios of the bodies hasn’t been specified yet.
This is because a general solution must work for any of the permissible ratios of masses of the bodies.
Restricting our analysis to cases where the mass of one of the 3 bodies is insignificant in comparison to the other 2 ensures a great deal of simplification.
The tiny mass of one the bodies means that its gravitational influence can be neglected.
This eliminates the terms involving the interaction between this object and the other two. The resulting differential equations are essentially the same as the equations resulting from a 2 body problem, just with an extra mass dancing around the other two as dictated by the combined effect of latter’s respective influence.
Equations describing the 3 body problem in Newtonian formulation
(Source : https://en.m.wikipedia.org/wiki/Three-body_problem)
Such a system, resulting from the reduction of one the bodies is called as a Reduced 3 Body System.
Following this reduction scheme, we can also consider that if the bodies are far enough apart, the solution to the 3 body problem (or an n-body problem for that matter) can be approximated as a sum of two (or n-1) 2-body problems.
This, however, defeats the original purpose.
Particular Solutions
Reduction by suitable mass ratio is the primary method of simplification.
But we can also consider special configurations where we can actually solve the problem. Such alternatives were first sought by Euler and Lagrange.
Euler (1767)
Euler imagined 3 bodies lying on a straight line.
Despite the masses being arbitrary, Euler was able to show that the bodies stayed on this line for suitable initial conditions.
The line, infact, would rotate about the center of mass of the bodies.
This results in periodic motions of all three bodies along their elliptical orbits.
Lagrange (1772)
Lagrange considered an equilateral triangle formed by the masses instead.
He showed that if the bodies were so positioned and moved along ellipses, for certain initial conditions, they always preserved their original configuration.
The solutions by Euler and Lagrange are particular solutions to the general 3 body problem.
These two families of solutions reveal 5 unique orbits in a 2 body system in which a third body’s motion, if introduced, can be described analytically.
These are called the Lagrange points.
Despite centuries of work by brilliant researchers and trusty computers, they are the only perfectly analytical solutions that exist for the 3 body problem. Lagrange points serve a crucial role in orbital and celestial mechanics, which might be discussed later in a separate article.
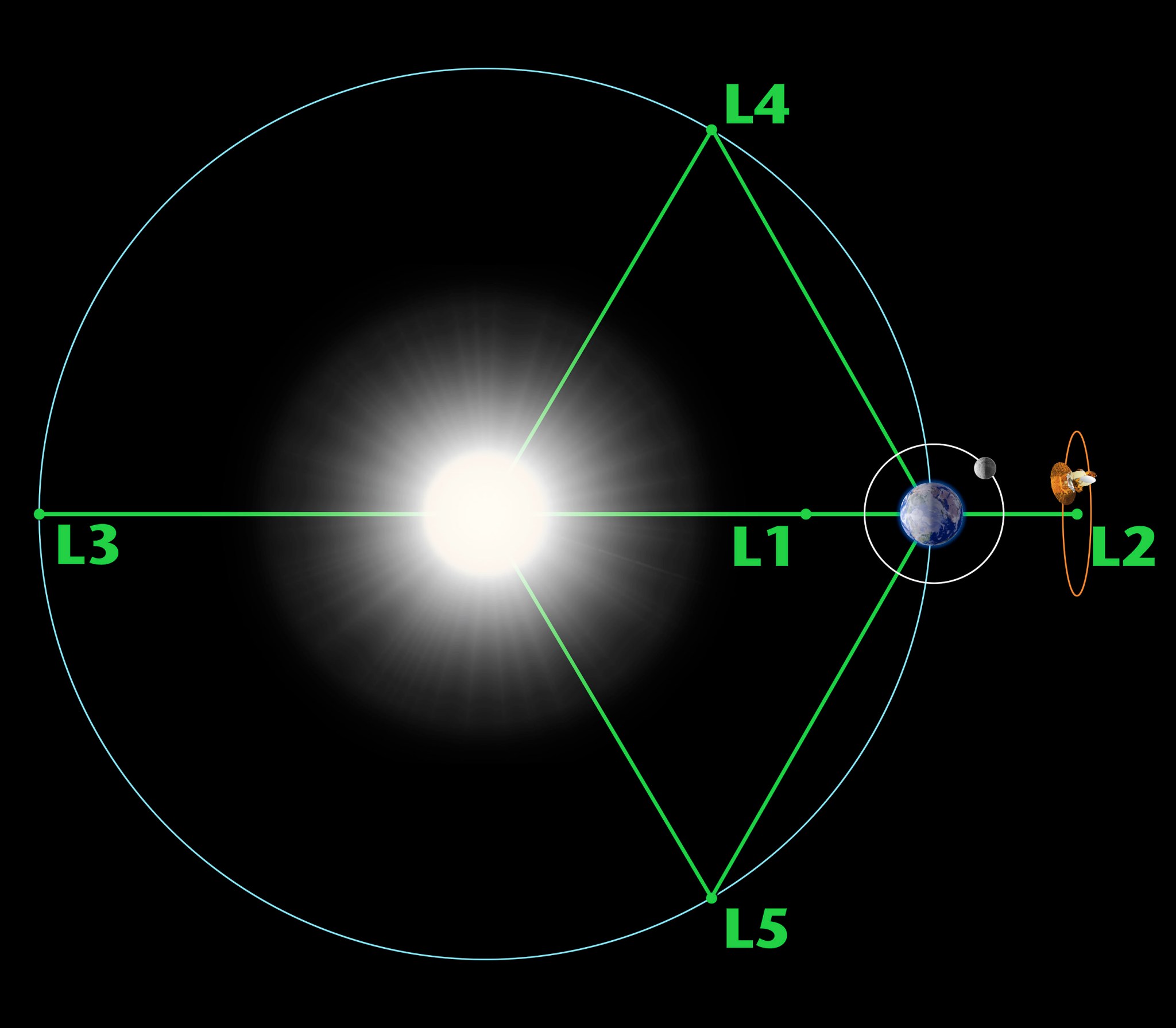
Lagrange points for the Sun-Earth system
(Source : https://science.nasa.gov/solar-system/resources/faq/what-are-lagrange-points/)
The periodicity of particular solutions sparked a revolution in the study of Circular Restricted 3 Body Problem (CR3BP) - reduced 3 body system restricted to move in circles.
Jacobi (1836) and Hill (1878)
Subsequent attempts aimed to capitalize on the advances made by Euler.
Using the synodic (rotating) coordinate system (originally introduced by Euler), Jacobi demonstrated that a quantity now called the Jacobi integral is conserved in the motion of any 3 bodies.
This integral, also referred to as the Jacobi constant, is the only known conserved quantity for the CR3BP.
George William Hill used this conserved integral of Jacobi’s to introduce the concept of zero velocity curves (ZVC), which represent a surface that a body possessing a given energy cannot cross, since it would have zero velocity on the surface.
This establishes regions in space where the bodies are allowed to move.
An even more specific case of the CR3BP, which Hill was interested in involved two masses which were much smaller than the first one (now known as the Hill problem).
This led to his discovery of a new class of periodic solutions.
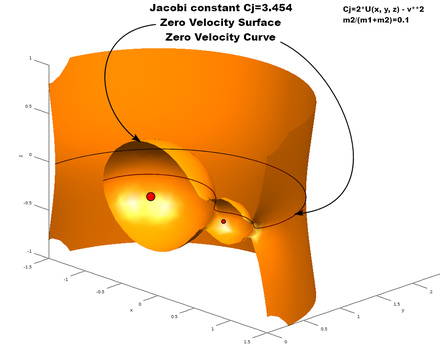
Zero Velocity Curves and Surfaces
(Source : https://en.m.wikipedia.org/wiki/Zero-velocity_surface)
Hill’s most essential work, however was his lunar theory, which came about two hundred years after the original formulation by Newton.
This theory, with some modifications, is still being used in celestial mechanics.
Poincaré
Poincaré headed this research program in the latter half of the nineteenth century.
In his trilogy of Les Méthodes Nouvelles de la Mécanique Céleste, Poincaré developed numerous novel methods to solve differential equations. These new methods allowed him to identify the unpredictability of the problem.
And it is this identification that led him to the phenomenon of chaos (which will not be discussed in the article).
Periodic Solutions
Poincaré’s methods could be used to study possible periodic orbits.
So he studied Hill’s problem and generalized his definition of periodic orbits. In the process, Poincaré was able to find initial conditions pertaining to special restricted 3 body systems.
He also worked on the existence of periodic solutions in dynamical systems with one degree of freedom.
This was extended by Bendixson who formulated and proved as well, a theorem now known as the Poincaré-Bendixson theorem, which gives a criterion for the existence of periodic solutions in such systems.
Poincaré’s advances gave way to systematic searches for periodic orbits in the 3 body problem, their classification and the stability of such orbits.
Singularities
In some differential equations for the system, solutions are abruptly terminated.
These are called singularities.
Singularities that arise due to collisions between the two or even all of the three bodies are called collision singularities.
Upon confirming of the presence of a singularity, the regularization method is used to eliminate them.
Regularization comes up frequently in another corner of physics - quantum field theory (QFT), where it is employed for a similar purpose. The fact that QFT is the most remarkably accurate theory mankind has ever constructed might give you an idea about the effectiveness of this mathematical technique.
Painlevé
Paul Painlevé was a mathematician who interestingly served twice as the Prime Minister of the Third French Republic.
He determined that these collisions were not just a kind of singularity, rather they were the only singularities that could crop up.
The French mathematician soon concluded that collisions can be excluded by setting certain initial conditions for which the equations of motion of the 3 body problem could perhaps be integrated using a power-series solution. In a power-series solution, one assumes a power series with unknown coefficients. This series is then substituted back into the differential equation to find a recurrence relation for the coefficients, thus helping us determine the assumed unknowns.
Power series in one variable
(Source : https://en.m.wikipedia.org/wiki/Power_series)
Painlevé may not have found such solutions himself, but his work had a profound impact on the academic community.
The regularization of collisions between two bodies was investigated further by Levi-Civita, Bisconcini and Sundman who also studied the rarer triple collisions and formulated theorems that allowed establishing conditions for such collisions.
Yet, the dreams of a general solution were still too far.
Infinite Series Solutions
Researchers recognized that finding closed-form solutions to the 3 body problem seemed impossible.
In mathematics, an equation is said to be a closed-form solution if it solves a given problem in terms of functions and mathematical operations from a given generally-accepted set. An infinite sum is not considered closed-form.
So they considered finding infinite series solutions instead. Painlevé and his contemporaries attempted to find such solutions but to no avail.
However, in 1907, a Finnish mathematician put the question to rest, once and for all.
Sundman’s General Solution
Karl Sundman was the only one who suceeded in finding this coveted series.
Sundman considered a double collision singularity and showed that it could be removed by introducing a regularizing variable defined in terms of time t.
He chose to represent the time of occurance of this singularity at τ.
Sundman also discovered that the coordinates of the three bodies could be expanded in powers of (t − τ)/2 and that he could use an analytical continuation to demonstrate that the expansion described correctly motions after the collision.
Analytic continuation is a technique in mathematics which provides a way of extending the domain over which a complex function is defined. It is most commonly applied to analytic functions determined near a point by a power series, just like the one present in Sundman’s case.
In this scenario, the energy remained unchanged, the areal velocity stayed constant, and the solutions were valid for t > τ and described motions correctly after each new double collision.
Note that the triple collisions were not allowed in this approach.
By defining more such variables and using regularisation transformations, Sundman arrived at a construction which guaranteed that the coordinates of the bodies, their mutual distances and time were analytic functions of one of the defined variables.
Periodic solutions to the 3 Body problem
(Source : https://en.m.wikipedia.org/wiki/Three-body_problem)
Given that the expansions of these functions are convergent, their different terms can be calculated once a certain number of them are specified.
Thus, these are complete solutions to the GENERAL 3 body problem.
Applications
A quick note.
Everything you just read, however elegant it may seem, is utterly useless.
See, besides the romantic notion of ‘putting a full-stop’, Sundman’s solution barely adds anything to the already procured knowledge about the 3 body problem. The convergence of Sundman’s series is pathetically slow.
So much so, that it requires millions of terms to find the motion of one body for insignificantly short durations of time.
Moreover, they are unfit for numerical calculations because of round-off errors. Thus, dishearteningly, they have ZERO practical applicability.
It is interesting to note that the general 3 body problem doesn’t seem to lend itself to much useful applications. This is owing to the fact that many of the complex configurations that we have studied for the 3 body systems simply don’t appear anywhere !
One configuration that did, however, turn out to practical was the restricted 3 body system.
Hence, this framework has been used to study various astronomical systems.
Space Missions
Spacecraft trajectories for satellite and lander space missions are the most evident examples.
NASA’s Apollo 8 - 10 missions to the Moon relied on accurate numerical solutions to the 3 body problem. So did their discovery missions - the Hubble Space Telescope, CHANDRA X-Ray Observatory, SPITZER Space Telescope, Kepler Space Telescope, and the James Webb Space Telescope.
Each one of these missions involves a different solution to restricted 3 body problem.
Earth-Moon-Spacecraft System
As the name suggests, the knowledge of this system comes in handy while maneuvering spacecrafts from Earth to the Moon or even between any 2 nearby planets.
However, space missions through the farther regions of the Solar System are rather complex and require the spacecraft trajectories to be designed by decoupling an n-body system into several 3 body systems. Further complications arise when the spacecraft moves in the vicinity of asteroids or other celestial objects with gravitational fields that are not sufficiently well-established.

Each mission is a different solution to the 3 Body problem
(Source : https://en.m.wikipedia.org/wiki/List_of_space_telescopes)
Decomposition of an n-body system involves non-coplanar 3 body systems.
For instance, the Earth-Sun-spacecraft and Earth-Moon-spacecraft systems are not necessarily coplanar for all times.
Hence, the 3D configurations must also be considered along with circular restrictions.
The planar motion of a spacecraft relative to two other masses which orbit each other is extremely complex, with non-linear effects due to the perturbation of the two bodies, for which no general analytical solution exists as of yet.
Consequently, the orbital analysis for any such spacecraft is based on sophisticated numerical methods.
Earth-Moon-Sun System
Unlike the previous application concerning satellites, this 3 body system has a BIG problem.
The masses of the Earth (10^24 kg) and the Moon (10^22 kg) differ by only 2 orders of magnitude. The separation between the two bodies (0.002543 AU) is quite small as well in astronomical terms.
This proximity induces reaction forces and tides that are not accounted for in the restricted 3 body problem.
Hill did make some progress in determining stability conditions for the Sun-Earth-Moon system. He had developed a general stability criterion based upon the balance of gravitational forces on a test particle between the Earth and the Sun.
This criterion has since been refined statistically through numerical simulation.
References
- https://www.scientificamerican.com/article/the-three-body-problem/
- The three-body problem by Z.E. Musielak and B. Quarles
- https://en.m.wikipedia.org/wiki/Jacobi_integral
- https://en.m.wikipedia.org/wiki/Zero-velocity_surface
- https://mathworld.wolfram.com/AnalyticContinuation.html


